Python+Pandasで平均値・中央値代入と線形回帰で欠損値に対処する話。

こんにちは、えんせきです。
今日はお仕事で東海道線からお送りします。熱海より西の東海道線初めて乗った気がします。

つまりなにしたの？

前回に引き続き、欠損値に対処していく。
平均値・中央値代入と線形回帰で欠損値に対する対処をPythonでやってみた。

前回はこちら
ensekitt.hatenablog.com

平均値・中値代入とは

欠損している値が含まれる系列の平均値とか中央値で埋める手法。分散が小さかったりすると手軽さの割りに効果的でおすすめ。

線形回帰による代入とは

相関の強い別の系列を使って欠損している系列の値を予想して埋める手法。MARに適用すると効果的でおすすめ。

実際にやってみる

データセットはまた東海クラスのみんな。*1
今回は無理やり相関が出るように作った。

# 分布の作り
## 数学と国語に負の相関がある
## 英語と国語に正の相関がある

columns = ['Name', 'English', 'Mathematics', 'Japanese']
names = ['kawasaki',
         'fujisawa',
         'kikukawa',
         'kanaya',
         'takatsuka',
         'totsuka',
         'okazaki',
         'ogaki',
         'mishima',
         'oofuna',
         'oiso',
         'ninomiya',
         'hayakawa',
         'toyohashi']
japanese = [min(100, int(np.random.normal(70, 10))) for i in range(len(names))]
math = [min(100, int(np.random.normal(140-j, 10))) for j in japanese]
english = [min(100, int(np.random.normal(j, 10))) for j in japanese]



plt.figure()
plt.ylabel("Japanese")
plt.xlabel("Mathematics")
plt.scatter(math,japanese)

plt.figure()
plt.ylabel("Japanese")
plt.xlabel("English")
plt.scatter(english,japanese)

tokai_class = pd.DataFrame([names, english, math, japanese]).T
tokai_class.columns = columns

# 欠損値を作る
# marで数箇所
tokai_mar = tokai_class.copy()
tokai_mar['Japanese'] = tokai_mar['Japanese'].replace(tokai_mar[tokai_mar['English']<62]['Japanese'], np.NaN)

tokai_mar

平均値代入の適用

# 平均値代入法(JapaneseのMARパターンの欠損に対応)
tokai_mean = tokai_mar.copy()
tokai_mean.Japanese = tokai_mar.Japanese.fillna(tokai_mar.Japanese.mean())

# 以下可視化
plt.title("Mean substitution")
plt.xlabel("Original")
plt.ylabel("with Substitution")
col = ['r' if c else 'b' for c in tokai_mar.Japanese.isna()]
plt.scatter(tokai_class.Japanese, tokai_mean.Japanese, c=col)

今回は真値がわかっているので比較してみた。
横軸に真値、縦軸に欠損したやつの代入値で代入したものは赤くしてある。
上振れ気味。

中央値代入の適用

# 中央値代入法(JapaneseのMARパターンの欠損に対応)
tokai_median = tokai_mar.copy()
tokai_median.Japanese = tokai_mar.Japanese.fillna(tokai_mar.Japanese.median())

# 以下可視化
plt.title("Median substitution")
plt.xlabel("Original")
plt.ylabel("with Substitution")
col = ['r' if c else 'b' for c in tokai_mar.Japanese.isna()]
plt.scatter(tokai_class.Japanese, tokai_median.Japanese, c=col)

今回は正規分布で作っちゃったのでほとんど平均値のときと変わらない。

回帰代入の適用

# 回帰代入法（JapaneseのMARパターンの欠損に対応）
tokai_reg = tokai_mar.copy()
from sklearn.linear_model import LinearRegression
reg = LinearRegression()
ja_isna = tokai_reg.Japanese.isna()
reg.fit(tokai_reg.loc[~ja_isna, ['English']], tokai_reg.loc[~ja_isna, 'Japanese'])
pred = reg.predict(tokai_reg.loc[ja_isna, ['English']])
tokai_reg.loc[ja_isna, 'Japanese'] = pred

# 以下可視化
plt.title("Linear Regression substitution")
plt.xlabel("Original")
plt.ylabel("with Substitution")
col = ['r' if c else 'b' for c in tokai_mar.Japanese.isna()]
plt.scatter(tokai_class.Japanese, tokai_reg.Japanese, c=col)

点数分布の作り方が今日これをやるためにやっているだけあって良い性能が出た。

plt.scatter(x=tokai_reg[~ja_isna].English, y=tokai_reg[~ja_isna].Japanese, c='b')
plt.scatter(x=tokai_reg[ja_isna].English, y=tokai_reg[ja_isna].Japanese, c='r', marker='v')
x = np.linspace(40, 100)
plt.xlabel('English')
plt.ylabel('Japanese')
plt.plot(x, reg.coef_[0] * x + reg.intercept_, c='g', linestyle='dashed')

回帰直線と合わせてどんな予測をもとにしたか確認する。

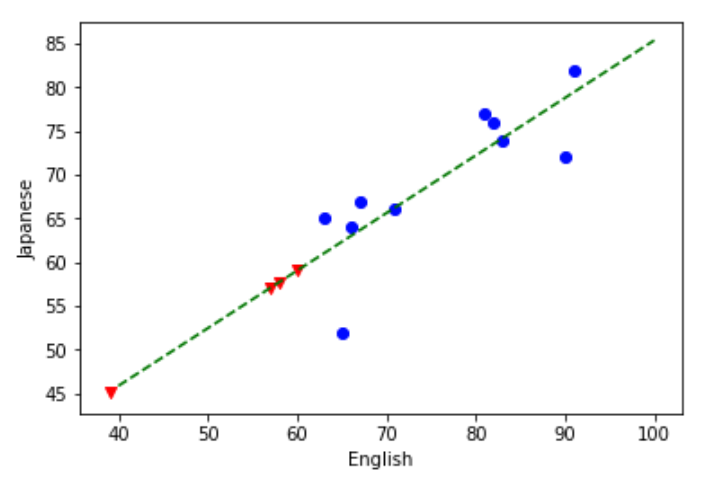
緑の破線が線形回帰で作ったやつで、赤い▼が線形予測で補完した値。

参考文献

pediatricsurgery.hatenadiary.jp
s0sem0y.hatenablog.com

*1:東海道線に揺られながらBlogを書いているのでこんなことになっている。